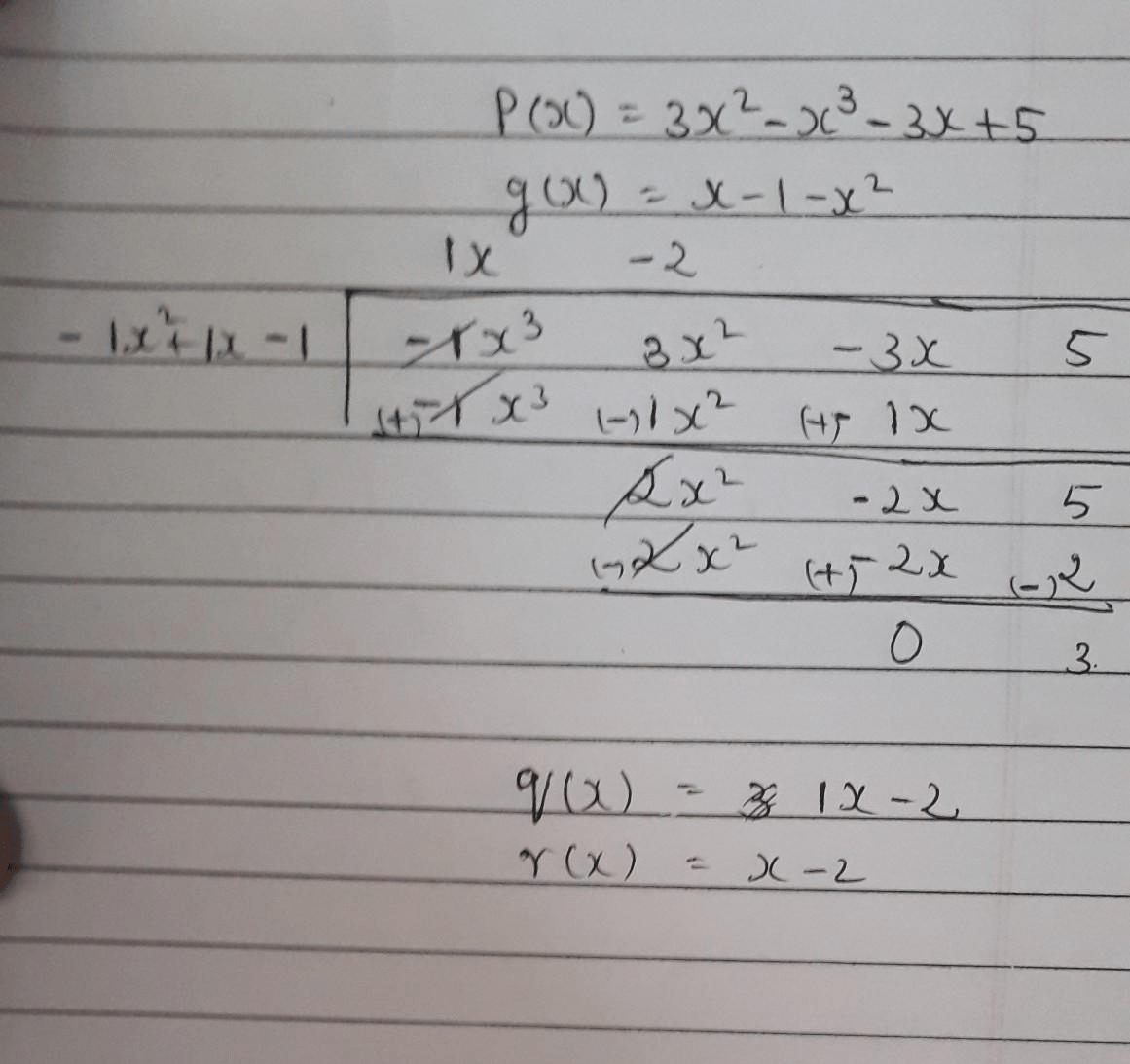In this module we will see how to arrive at this factorisation.
Similarly we can factor the cubic x 3 − 6 x 2 + 11 x − 6 as ( x − 1)( x − 2)( x − 3), which enables us to show that the solutions of x 3 − 6 x 2 + 11 x − 6 = 0 are x = 1, x = 2 or x = 3. The quadratic x 2 − 5 x + 6 factors as ( x − 2)( x − 3). How these things might be performed with algebraic expressions of higher degree. We can factor quadratic expressions, solve quadratic equations and graph quadratic functions, the obvious question arises as to Indeed a quadratic is a polynomial of degree 2. Polynomials represent the next level of algebraic complexity after quadratics.